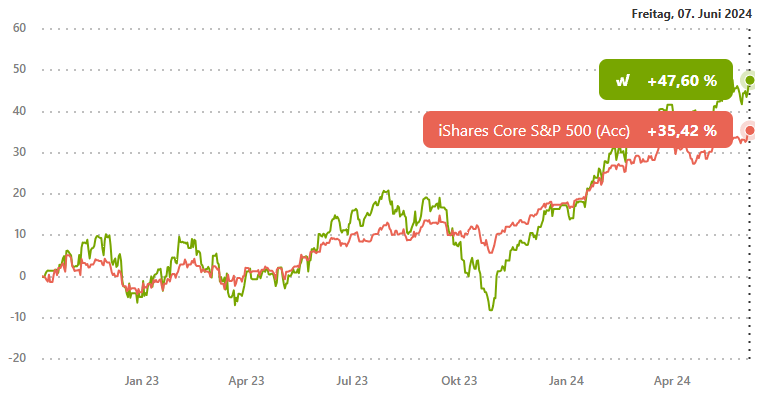
Auf Finanzseiten wie finanzen.net und verschiedenen Fondsplattformen bin ich oft auf einen Wert gestoßen: R². In diesem Artikel werde ich die verschiedenen Aspekte dieses Wertes beleuchten und Ihnen helfen, seine Bedeutung und Anwendung in der Finanzwelt besser zu verstehen.

R zum Quadrat, oder R², ist eine wichtige statistische Metrik in der Welt der Finanzen, die dazu dient, die Beziehung zwischen einem Portfolio und seinem Benchmark-Index zu quantifizieren.

Was ist R²?

R² ist ein Wert zwischen 0 und 1, der angibt, wie gut die Schwankungen der Renditen eines Portfolios durch die Renditen seines Benchmark-Index erklärt werden können. Ein hoher R zum Quadrat-Wert (nahe 1) bedeutet, dass die Renditen des Portfolios eng mit denen des Benchmarks korrelieren, während ein niedriger Wert (nahe 0) auf eine geringe Korrelation hinweist.

Die Bedeutung von R²

1. Portfolioanalyse: R² ist ein nützliches Werkzeug für Portfolioanalysten, um herauszufinden, wie genau ein bestimmtes Portfolio die Benchmark nachbildet. Ein hoher R²-Wert kann darauf hindeuten, dass ein Fondsmanager eine passive Anlagestrategie verfolgt, die darauf abzielt, die Benchmark so genau wie möglich nachzubilden.
2. Performancebewertung: Investoren können R² verwenden, um die Leistung von Investmentfonds oder Portfolios zu bewerten. Wenn ein Fonds einen hohen R²-Wert aufweist, kann er als gut verwaltet betrachtet werden, wenn das Ziel darin besteht, die Benchmark zu replizieren.
3. Diversifikation: R² kann auch bei der Diversifikation eines Portfolios helfen. Ein Portfolio aus verschiedenen Anlageklassen mit niedrigen R²-Werten zueinander kann dazu beitragen, das Gesamtrisiko zu reduzieren, da die verschiedenen Anlagen nicht stark miteinander korrelieren.

Die Grenzen von R²

Obwohl R² ein nützliches Instrument ist, hat es seine Grenzen:

1. Keine Information zur Outperformance: R² gibt keine Informationen darüber, ob ein Portfolio die Benchmark über- oder unterperformt. Ein Portfolio kann eine hohe Übereinstimmung mit der Benchmark haben, aber dennoch schlecht performen.
2. Stabilität der R²-Werte: R²-Werte können im Laufe der Zeit schwanken. Ein Fondsmanager, der versucht, die Benchmark genau nachzubilden, kann aufgrund von Marktschwankungen und Gebühren Schwierigkeiten haben, einen konstant hohen R²-Wert aufrechtzuerhalten.

Verwendung von R² in der Praxis

1. Fondsauswahl: Investoren können R zum Quadrat verwenden, um Investmentfonds auszuwählen, die ihren Anlagezielen entsprechen. Wenn ein Anleger beispielsweise eine passive Anlagestrategie verfolgen möchte, kann er nach Fonds mit hohem R² suchen.
2. Risikomanagement: R² kann dazu beitragen, das Risiko eines Portfolios besser zu verstehen. Wenn ein Portfolio hohe R²-Werte zu verschiedenen Anlageklassen aufweist, kann dies auf eine geringere Diversifikation hinweisen und somit auf ein höheres Gesamtrisiko.
3. Portfoliooptimierung: Portfolioanalysten verwenden R², um die optimale Allokation von Vermögenswerten in einem Portfolio zu bestimmen. Ein Portfolio, das verschiedene Anlageklassen mit niedrigen R²-Werten kombiniert, kann dazu beitragen, das Risiko zu reduzieren und die Rendite zu steigern.

Berechnung von R²

R² wird üblicherweise als Prozentsatz ausgedrückt und bewegt sich im Bereich von 0% bis 100%.

Die Berechnung von R² erfolgt nach folgender Formel:

R2=1−(SST/SSR)​​​

Hierbei stehen SSR (Summe der quadrierten Residuen) und SST (Totale quadrierte Abweichung) im Mittelpunkt der Berechnung.

SSR (Summe der quadrierten Residuen) repräsentiert die Gesamtsumme der quadrierten Unterschiede zwischen den beobachteten Werten (yi) und den vorhergesagten Werten (ŷi) des statistischen Modells. Dies kann mathematisch wie folgt ausgedrückt werden:

SSR=∑i=1​(yi−ŷ​i​)^2

SST (Totale quadrierte Abweichung) hingegen stellt die Summe der quadrierten Unterschiede zwischen den beobachteten Werten (y) und dem Durchschnitt der beobachteten Werte (ȳ) dar. Dies kann mathematisch wie folgt ausgedrückt werden:

SST=∑i=1(yi​−ȳ)^2

Fazit

R², oder R zum Quadrat, ist ein leistungsstarkes Werkzeug in der Welt der Finanzen, das dazu beiträgt, die Beziehung zwischen einem Portfolio und seinem Benchmark-Index zu quantifizieren. Es kann bei der Portfolioanalyse, der Performancebewertung, der Diversifikation und der Portfoliooptimierung nützlich sein.

Allerdings ist es wichtig, R² immer im Zusammenhang mit anderen wichtigen Portfolio-Kennzahlen und -Metriken zu betrachten, um eine umfassende Beurteilung der Portfolio-Performance zu ermöglichen. Weitere wichtige Portfoliokennzahlen sind:

1. Beta-Faktor
2. Information Ratio
3. Tracking Error
4. Capture Ratio
5. Maximaler Verlust
6. Korrelation
7. Sharpe-Ratio

Die Kombination dieser Kennzahlen bietet die Grundlage für eine Analyse des Fonds oder der aktiven Strategie und ermöglicht es Investoren, fundierte Entscheidungen über ihre Anlagen zu treffen. Aus diesem Grund stellen viele Fondsvergleichsplattformen (z.B. finanzen.net; morningstar) diese Werte zur Verfügung.